BNPO : Bellman with Natural and Policy Optimization

B(N)PO : Combined Off and On Policy Algorithm

Contribution

Introduction of B(N)PO, Bellman with (Natural and) Policy Optimization, algorithm which allows to mix various RL algorithms like DDPG and PPO into one learning process (to train single neural network!), which opens the door for potentially benefit from both of the worlds ( Off-policy and On-policy RL algorithm family ). While at first part of this post i will go trough PPO algorithm and its limitation when it comes to compatibility with HER and way around how to make it work, which was later inspiration behind BNPO, and reason why I keep testing against Reacher environment.

• This work is third iteration of my wheeler project, and again I used Reacher UnityML environment for testing.

PPO and HER

Policy Proximal Optimizations, PPO, is algorithm of choice for many companies and RL practicioners, due its simplicity and because it just works! PPO is on-policy gradient method which utilize importance sampling, therefore it does not use replay buffer, or better to say: does not use replay buffer of size bigger than few learning rounds of experience due irrelevancy of old experience to this method. Due to this drawback it is challenging, or not possible, to use PPO with other algorithms whose change distribution of experience, therefore expectation in policy gradient, in unprincipled way. Hindisght Experience replay, HER, is example of algorithm difficult to use with PPO, and so is described at OpenAI Rquest for research. In following part of post i will tackle this problem and propose some approaches how to go away with it.

PPO, Policy Gradient and Expectation

At first lets draw more bit simplified description of PPO without cliping :

\begin{aligned} \sum_\tau \mathbb{P}(\tau, \theta) \frac{\mathbb{P}(\tau, \theta')}{\mathbb{P}(\tau, \theta)} R(\tau) \end{aligned}

When i first read in OpenAI’s request for research On-Policy HER section, I did not understood well why it is a problem for HER to work with PPO. So, to see it more clearly, lets write down how it will looks like when we use HER with PPO :

\begin{aligned} \sum_\tau \mathbb{P}(\tau, \theta) \frac{\mathbb{P}(\tau’, \theta’)}{\mathbb{P}(\tau, \theta)} R(\tau’) \end{aligned}

Why is this a problem ? Well, most important here is how Monte Carlo and Imporatance Sampling approach works. Now lets review Policy Gradient :

\begin{aligned} \nabla_\theta J(\theta) &= \nabla_\theta E_\pi[R(\tau)] \\ &=\nabla_\theta \sum_\tau \mathbb{P}(\tau,\theta)R(\tau) \\ &= \sum_\tau \nabla_\theta \mathbb{P}(\tau, \theta) R(\tau) \\ &= \sum_\tau \mathbb{P}(\tau, \theta) \frac{\nabla \mathbb{P}(\tau, \theta)}{\mathbb{P}(\tau, \theta)}R(\tau) \\ &= E_\pi[\frac{\nabla \mathbb{P}(\tau, \theta)}{\mathbb{P}(\tau, \theta)}R(\tau)] \end{aligned}

To put it simply, in order to use Monte Carlo we need to have distribution to sample from and this distribution needs to be representative w.r.t. policy and its interaction with environment ( rewards, transition probabilities ). And that is terribly broken by HER, as rewards are not coherently collected w.r.t. to expaction we summing over and old policy probabilities are for original goal ( transitions are obsolete ):

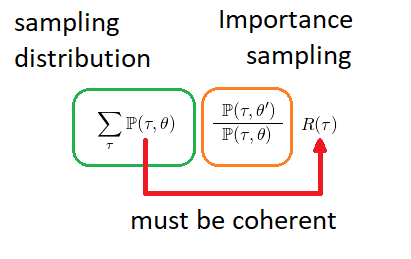
Why it works for DDPG then ? Because here policy objective is take action which maximize expected reward for given state action pair directly (Bellman equations). Therefore instead of doing expectation over policy distribution, we borrow DQN approach, however to get max over all Q-functions from single state in Bellman equation, which is unfeasible in continuous case, we will try to average gradients, which maximize Q function given state-action pair, over experienced replay buffer :

\begin{aligned} \nabla_\theta J(\theta) &= \frac{1}{N} \sum_{s} \nabla_a Q^\mu(s, a) \nabla_\theta \mu_\theta(s) \rvert_{a=\mu_\theta(s)} \end{aligned}

In another words, in order for PPO to work it needs estimate via true distribution, by definition, and for that use is leveraged Monte Carlo method. However, as far as DDPG is concerned, Bellman equations needs to work over distribution, no necessary be the true one (and therefore HER work fine). But working over uniform distribution of long horizon of experience can introduce bias for DDPG (means also with HER), interestingly there is recent research which can tackle this, which I will describe in other section.

Shifting goals

However there it comes to Reacher environment from UnityML

Obvious difference is that target keep moving, that itself is however not too significant change w.r.t. MuJoCo Reacher. Here also we can utilize HER, and solve environment in quite good 10~12 full episodes ( i cut episode to 60 steps chunks instead of 1000, therefore in my notebooks it shows up number 180 episodes ~ those are short ones ). But most intriguing is that it was solved by HER + PPO! Now, how is this possible ?

class ReacherHER(HER):
    def update_goal(self, rewards, goals, states, states_1, n_goals, n_states, actions, her_step_inds, n_steps):
        MAX_HER_STEP = 1
        gid, delta = 0, 0
        h_rewards, h_goals, h_n_goals = rewards, goals, n_goals
        for i, (g, s, n_g, n, u, step) in enumerate(zip(goals, states, n_goals, n_states, her_step_inds, n_steps)):
            her_active = bool(sum(her_step_inds[(i-MAX_HER_STEP) if MAX_HER_STEP < i else 0:i]))

            if not her_active and u: # we will set-up new goal
                delta = 0 # now lets select new goals from trajectory of goals!
                gid = random.randint(0, len(goals)-self.n_step-MAX_HER_STEP-1)
                
            if her_active or u:
                delta += 1
                g, n_g = goals[gid+delta], goals[gid+delta+step]
                
            h_rewards[i] = f_reward(s, n, g)
            h_goals[i], h_n_goals[i] = g, n_g

        return ( h_rewards, h_goals, states, h_n_goals, n_states )

As I mention, moving target is not significant difference nor reason why PPO here work with HER. But when we look closely:

• target is moving on same trajectory!
• HER goal, target position, is selected from original but shifted set of targets ( tau+ )! \begin{aligned} \sum_\tau \mathbb{P}(\tau, \theta) \frac{\mathbb{P}(\tau^+, \theta’)}{\mathbb{P}(\tau, \theta)} R(\tau^+) \end{aligned}

As you can see I reused formula from PPO+HER but with slight difference replacing tau’ with tau+, changing superscripts does not make it any different, but here changing superscript means we changed strategy of choosing goals. But still formula is not well aligned, in terms of denominator is inconsistent, using old trajectory probabilities. While it seems to works as it is, it can be fixed easily by pre-calculating (log)probabilities per goal in advance as we have hardcoded selection ( we pick goals only from set of sampled targets by environment per trajectory ), which is not necessary too much of overhead when you either shrink episode length or you shrink your selection of targets to some fixed N which will be hyperparameter to tune. And as new trajectory is just ‘shift’-ed one from original, then expected value over this formula seems to be representative enough.

And that seems to be the most significant difference. With MuJoCo Reacher HER baseline, targets was chosen from trajectory of states which was achieved ‘arbitrary’ by interacting policy with environment, and therefore introducing it to policy gradient will by default change collected experience in unprincipled way, which on the other hand seems not to be so much prevelant problem when following are true :

• targets (= goals) per step in environment are not stationary
• trajectory of targets have similar pattern ( circle in our case )

However several benchmarks are missing to cover validity of this observation. As same targets trajectory pattern could lead to policy learning dynamics of that trajectory and using little to no information from goal state. Which in turn could also explain why PPO + HER working here ( by surpassing / ignoring HER ). However, shifting goals approach pinpointing that how to select goals can play interesting role in HER ( and further PPO application ), as well as environment update, in this example towards moving target with same pattern, may potentially leads to result we are interested in ( to hit stationary target, though as I mention this is untested ). Some tests performed for this approach are listed in last section ( see PPO, PPO no her no fs, PPO no her but fs ).

BNPO

Another way to solve problem of HER breaking premises of PPO is simple not to use HER for PPO at all, but how then benefit from PPO features ? That is where DDPG comes back into the picture. My first attempt was to force DDPG + PPO cooperate, trough shared experience and part of network, you can see more at my previous blog post. However in this project I come with slightly different idea to turn DDPG less deterministic and more PG driven by trying to maximize :

\begin{aligned} \mathbb{E}[Q(s, \mu, \sigma )) \rvert_{\mu, \sigma\sim\pi_\theta(s)}] \end{aligned}

for DDPG Actor it results in classic PPO Head, where as output are provided mean and scale, which basically introduce Normal distribution and diminish D for deterministic from DDPG ( and that’s partially why I called out this project as algorithm with new name instead of framework like i did with (re)wheeler ). And as for Critic it means, in order to backpropagate to DDPG Actor, that it must accept not state and action pair, but state, pi-mean, pi-scale triplet as an input, and no taken action is provided! As this diverge from standard approach, it creates an opening space for failing in both DDPG and PPO, therefore i was doing brief tests if this drastically affect their applicability as you can check in last section (see PPO and DDPG). Seems it does not have drastic (if any) adversial effect on those.

Following this approach, and you can see where I am coming at, we can train single neural network once a time with DDPG once a time with PPO. And if this is feasible, then we can turn on HER only for DDPG and let PPO smooth learning w.r.t. newly sampled trajectories. To further demonstrate if this new algorithm is feasible I empirically select architecture where :

• BPO (PPO + D(D)PG cooperation with Q(state, mean, scale) ) solve environment quite efficiently
• either PPO or DDPG alone will struggle

However even following configuration does not cover second requirement, as PPO is too efficient for this environment, comparing to DDPG, at least i was not able to tune DDPG to be efficient enough, and almost with any PPO configuration it simple outperforms DDPG by quite a margin. That is one of the reason I need to switch to different environment where PPO struggle or is unable to solve (when combine with HER for example), like those from MuJoCo, though I need to work there abstraction layers for better scaling of mujoco environments and get a licence to test it more efficiently, as for that it is on my TODO list. Therefore this setup just shows that those two algorihm can converge to sucessfull result.

BS = 512
PPOBS = 2048
bpo_brain = [

        BrainDescription( # PPO smoothing
            memory_size=20 * MAX_STEPS * 5, batch_size=PPOBS, 
            
            optim_pool_size=(MAX_STEPS * 80 * 10) // 3,
            optim_epochs=1, optim_batch_size=1*PPOBS,  recalc_delay=3,
            
            lr_actor=1e-3, learning_delay=1*MAX_STEPS, learning_repeat=6,
            sync_delta_a=3, sync_delta_c=1, tau_actor=1e-1, tau_critic=1e-1,
            bellman=False, ppo_eps=2e-1, natural=False, mean_only=False, separate_actors=True),

        BrainDescription( # D(D)PG HER exploring
            memory_size=20 * MAX_STEPS * 200, batch_size=BS, 
            optim_pool_size=70000, optim_epochs=2, optim_batch_size=3*BS, recalc_delay=5,
            lr_actor=3e-5, learning_delay=10, learning_repeat=4,
            sync_delta_a=1, sync_delta_c=1, tau_actor=1e-1, tau_critic=1e-1,
            bellman=True, ppo_eps=None, natural=False, mean_only=True, separate_actors=False),

]

And this architecture do actually the job, in terms of solving environment with cooperation, as you can see in last section (see BPO). As for performance concerned, I did several hacks for replay buffer which I further described in another post, and it did not have much of slow down ( depends how much you want to recalculate in buffer and how expensive is HER goal selection, but that trade off depends on you, and can be further optimized ) in my tests I experienced about 10-20% slowdown comparing vanilla to PPO in my implementation, i used recalc_delay=2.

Importance Resampling

Importance Resampling(IR) idea is quite straightforward : \begin{aligned} \mathbb{E}[\nabla_{\theta}(A)|A\sim\pi_{behaviour}] \end{aligned}

Previous formula represent what we are doing in off-policy settings, but here is what we actually aiming for : \begin{aligned} \mathbb{E}[\nabla_{\theta}(A)|A\sim\pi_{target}] \end{aligned}

Therefore solution is is to update sampling mechanism in a way we would actually been doing what we really aim for. And when we look at Prioritized Experience Replay(PER), we can actually get idea how to use PER algorithm for Importance Resampling, with one slight difference (for more in depth explanation please refer to IR paper / slides ) : \begin{aligned} \rho = \frac{\pi_{target}}{\pi_{behaviour}} \end{aligned} \begin{aligned} \frac{\rho_i}{\sum^{|PER|}{p_j}} \end{aligned}

We avoid using TD error as our priority indicator, and exchange it with fraction of probabilities (rho), which we can represents as how more likely our new(target) policy will come with particular transition than the old(behaviour) one. And this nicely works with our B(N)PO idea, where we enabled D(D)PG work over distributions, and therefore Importance Resampling will introduce ‘true’ distribution, instead of uniform one, and should be able to reduce potential bias. And therefore no need to re-weight it afterwards as was done in case of using PER algorithm itself. As a final note, worth to mention that it could be quite performance overhead to keep IR fraction representative overtime, though in our implementation of replay buffer it is quite efficient and I will describe it in next post.

Detached policy targets architecture

One of interesting features of training, is that I use target and explorer networks for Actor ( actually also for critic but that is not important for now ), while explorer policy network is shared ( is used in all interaction with environment and updated by both algorithms ), target networks can be separated, by detach_actors switch, per algorithm ( DDPG, PPO, or else ). Therefore algorithm interaction can occur at two places ( separate_actors switch ):

• only trough sharing same explorer policy network
• or also by explorer network updates, which can take into account both target networks ( random selection of one per learning step ) when calculating baseline for advantage function, but final explorer network learning update is specific for particular algorithm

        if separate_actors: # how we want to interact between algorithms ( if detached targets )
            i = tind % len(self.ac_target.actor)
        else:
            i = random.randint(0, len(self.ac_target.actor)-1)

        a_i = tind % len(self.ac_explorer.actor)
        cind = tind % len(self.ac_target.critic)

        with torch.no_grad():
            n_qa, _ = self.ac_target(n_goals, n_states, n_memory, cind, i, mean_only)
        td_targets = n_rewards + n_discounts * n_qa

        qa, dists = self.ac_explorer(goals, states, memory, cind, a_i, mean_only)

# here specific algorithm is used ~ D(D)PG / PPO / ..
        pi_loss = backward_policy(qa, td_targets, probs, actions, dists)

        self.meta_update(
                tind,
                self.ac_explorer.actor[a_i].parameters(),
                self.ac_target.actor[tind % len(self.ac_target.actor)],
                tau_actor)

However this feature need to be putted further into testing and evaluate if it can have significant effect on learning or not.

Natural part

Modifying DDPG for output distribution, instead of deterministic action, opens up space for using Natural Gradient over DDPG gradients! And that is why N in BNPO. I studied several works for Natural Gradients, did go trough different implementations and ended up implemented this feature, using lot from TRPO code for conjugate gradients and line search, but did not draw any conclusion about it yet. And that is why B(N)PO. To be honest, while implemented, it is almost completely untested and waiting for further work on that. You can try to turn on natural=True flag in some notebook, i recommend for DDPG algorithm as surrogate loss is kind of hardcoded now, and experiment with it.

Implementation details

I encourage you check in code by yourself. Important stuffs you may want to look at :

• credit(.py) : Credit assignment, option to select for example HER approach, and turn it on for specific part of algorithm
• mean_only : option to select which part of algorithm will not backpropagate trough scale of policy(mean, scale)
• stable_probs : one can experiment with distributions for importance sampling ( by default explorer distribution is used, but can be changed to target one )
• separate_actors : method how to learn target networks ( basically where to draw line of interaction of detached targets : by common explorer network only, or take into account also other target to not diverge too far from it )

Conclusion

Due to lack of proper testing and benchmarking this project basically proves nothing. On the other side, it raising question of using this methodology for mixing On-Policy and Off-Policy Reinforcement Learning algorithms and make use of the best from those two worlds. Same time shows that methods like HER can be used for on-policy algorithms, like PPO, when we little bend our methods and view of problem. In this particular scenario, it tells us while we can not directly change expectation, we can shift it to some degree, and it will do the job.

Jupyter notebooks

Above mentioned notebooks :

• BPO ( demonstration of this technique : merging DDPG + PPO into single Actor with Critic consisting of Q(state, mean, scale) )
• PPO ( best performing method for Reacher environment I come with, consisting of two cooperating PPO algorithms ~ differs in hyperparameters )
• PPO no HER no FS w/o her and w/o floating step
• PPO no HER but FS w/o her but with floating step
• DDPG ( D(D)PG with Critic Q(state, mean, scale), i have always problems to run DDPG on this environment more effectivelly, seems good take off at begining, but hard to breaktrough to higher reward values )
• ReWHEELER ( Previous approach of cooperation DDPG + PPO trough shared experience and part of network, works, but was terribly slow due to replay buffer approach and limitation, though it could be dramatically optimized with my current replay approach. Worth of considering to experiment with as well )

For pre-trained weights let me know (twitter / github) i will share with you, but should be not a problem to train it by yourself. In anyway dont hesitate to ping me. Actually for this project I did not save weights, but I can do it if you query me for it.

Note: I may have done mistake in formulas or phrasing, if you catch one of those or have any comment / advice, please let me know ~ twitter, github, will appreciate it! Reacher Environment informations, download links, you can find here